Равносторонний треугольник - это особый вид треугольника, обладающий уникальными свойствами. Рассмотрим подробно его угловые характеристики.
Содержание
Основные свойства равностороннего треугольника
- Все три стороны равны между собой
- Все три угла равны между собой
- Является частным случаем равнобедренного треугольника
- Обладает тремя осями симметрии
Угловые характеристики
| Характеристика | Значение |
| Сумма внутренних углов | 180° |
| Величина каждого угла | 60° |
| Сумма внешних углов | 360° |
Доказательство суммы углов
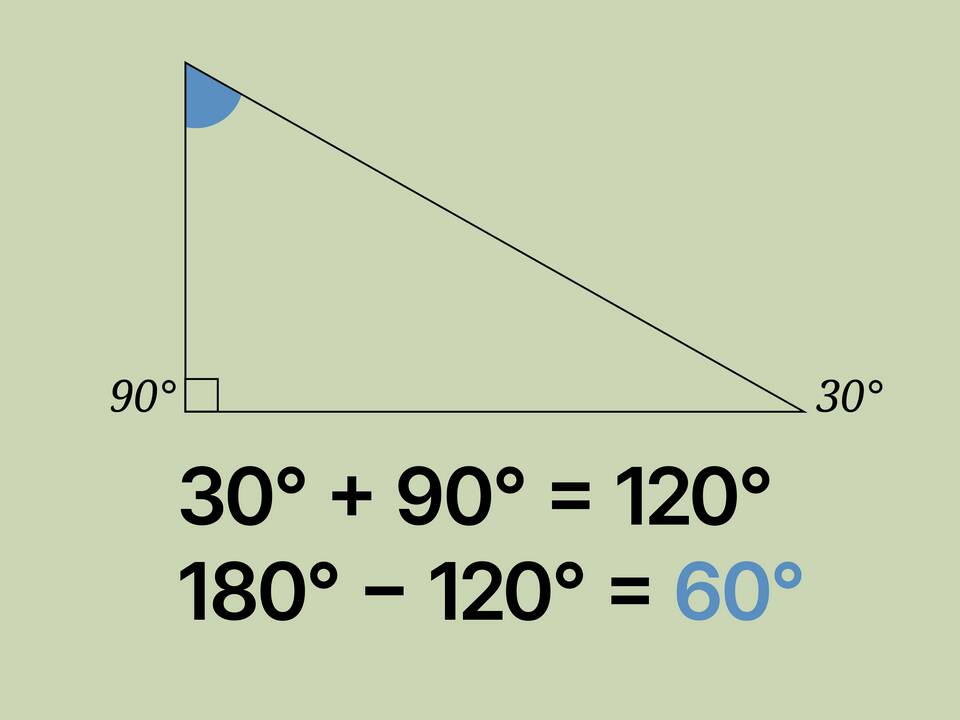
Для любого треугольника, включая равносторонний, сумма внутренних углов равна 180°. Это доказывается следующим образом:
- Проведем прямую, параллельную одной из сторон треугольника
- Образовавшиеся углы при параллельных прямых будут равны углам треугольника
- Сумма углов на прямой равна 180°
- Следовательно, сумма углов треугольника также равна 180°
Особенности равностороннего треугольника
Расчет величины каждого угла:
Поскольку все углы равны, а их сумма составляет 180°, то каждый угол равен:
180° ÷ 3 = 60°
Следствия из этого свойства:
- Равносторонний треугольник всегда остроугольный
- Все его углы меньше 90°
- Не может быть прямоугольным или тупоугольным
Практическое применение
| Область | Применение |
| Архитектура | Использование в устойчивых конструкциях |
| Инженерия | Создание равномерно нагруженных структур |
| Дизайн | Создание гармоничных композиций |
Сравнение с другими треугольниками
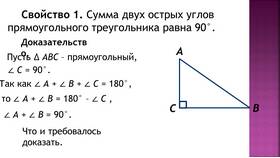
- В прямоугольном треугольнике: один угол 90°, сумма двух других - 90°
- В тупоугольном треугольнике: один угол >90°, сумма двух других <90°
- В равнобедренном треугольнике: два угла равны
Знание свойств равностороннего треугольника, включая сумму его углов, является фундаментальным для геометрии и находит применение во многих практических областях.