В геометрии существует важное утверждение о сумме острых углов в прямоугольном треугольнике. Рассмотрим математическое доказательство этого положения.
Содержание
В геометрии существует важное утверждение о сумме острых углов в прямоугольном треугольнике. Рассмотрим математическое доказательство этого положения.
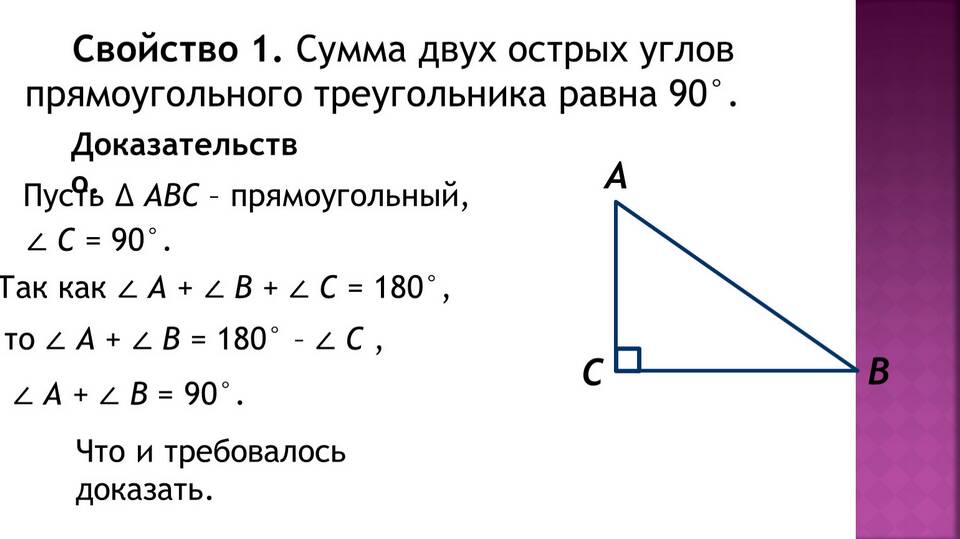
Формулировка теоремы
Сумма двух острых углов в прямоугольном треугольнике равна 90°.
Дано:
- Треугольник ABC
- ∠C = 90° (прямой угол)
- ∠A и ∠B - острые углы
Доказательство:
- По теореме о сумме углов треугольника: ∠A + ∠B + ∠C = 180°
- Подставим значение прямого угла: ∠A + ∠B + 90° = 180°
- Перенесем 90° в правую часть уравнения: ∠A + ∠B = 180° - 90°
- Получаем: ∠A + ∠B = 90°
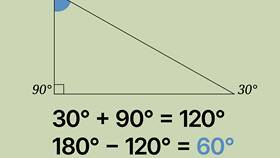
Геометрическая иллюстрация
| Угол | Значение |
| ∠A | Острый угол (меньше 90°) |
| ∠B | Острый угол (меньше 90°) |
| ∠C | Прямой угол (ровно 90°) |
Таким образом, мы доказали, что сумма двух острых углов в прямоугольном треугольнике всегда равна 90°. Это свойство широко используется при решении геометрических задач и доказательстве других теорем.
Следствия из теоремы
- Оба острых угла в прямоугольном треугольнике всегда дополняют друг друга до 90°
- Если один острый угол известен, второй можно найти вычитанием из 90°
- В равнобедренном прямоугольном треугольнике оба острых угла равны по 45°
